Exercícios Sobre Definição De Função – Exercícios Mundo Educação: mergulhe nesse universo de funções matemáticas! Vamos explorar diferentes tipos de funções, desde as lineares até as exponenciais, desvendando seus domínios, contradomínios e imagens. Prepare-se para dominar conceitos como funções injetoras, sobrejetoras e bijetoras, e a representação gráfica de funções. Através de exemplos práticos e exercícios resolvidos, você vai construir uma base sólida para entender o funcionamento e as aplicações das funções matemáticas.
Dominar o conceito de função é fundamental para o sucesso em matemática e áreas afins. Este guia prático oferece uma abordagem passo a passo, com exemplos claros e concisos, facilitando a compreensão de temas complexos. Aprenderemos a identificar o domínio e a imagem de uma função, realizar operações entre funções e compreender a representação gráfica, tudo isso com o objetivo de consolidar seus conhecimentos e prepará-lo para desafios mais complexos.
Tipos de Funções e Exemplos: Exercícios Sobre Definição De Função – Exercícios Mundo Educação
A compreensão dos diferentes tipos de funções matemáticas é fundamental para diversas áreas, desde a física e engenharia até a economia e a computação. Cada tipo apresenta características únicas em sua fórmula, comportamento gráfico e aplicações práticas. A seguir, exploraremos alguns dos tipos mais comuns, organizados por crescente complexidade.
Funções Lineares, Quadráticas e Exponenciais
As funções lineares, quadráticas e exponenciais representam classes importantes de funções com comportamentos distintos e ampla aplicabilidade em diversos contextos. A tabela abaixo resume suas características principais.
| Tipo de Função | Fórmula | Exemplo Numérico | Representação Gráfica |
|---|---|---|---|
| Linear | f(x) = mx + b | f(x) = 2x + 1 (Se x = 2, f(x) = 5) | Uma reta com inclinação ‘m’ e intercepto ‘b’ no eixo y. Uma inclinação positiva indica uma reta crescente, enquanto uma inclinação negativa indica uma reta decrescente. |
| Quadrática | f(x) = ax² + bx + c | f(x) = x²
|
Uma parábola. Se ‘a’ > 0, a parábola abre para cima, com um ponto mínimo; se ‘a’ < 0, a parábola abre para baixo, com um ponto máximo. |
| Exponencial | f(x) = abx | f(x) = 2x (Se x = 3, f(x) = 8) | Uma curva que cresce ou decresce exponencialmente. Se ‘b’ > 1, a função cresce exponencialmente; se 0 < 'b' < 1, a função decresce exponencialmente. A curva nunca intercepta o eixo x, a menos que a seja 0. |
Funções Injetoras, Sobrejetoras e Bijetoras
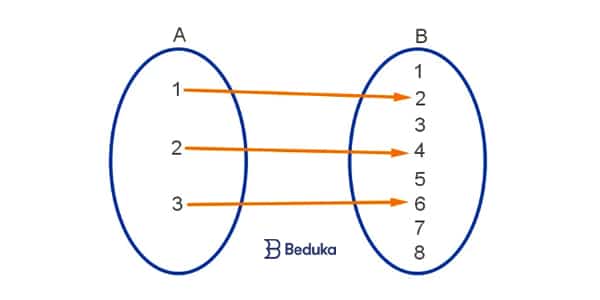
A classificação de funções em injetoras, sobrejetoras e bijetoras baseia-se na relação entre os elementos do domínio e da imagem. Estas propriedades são cruciais em diversas áreas da matemática, como álgebra abstrata e teoria dos conjuntos.Um exemplo para ilustrar: considere uma função f que mapeia um conjunto A (domínio) para um conjunto B (contradomínio/imagem).Uma função é injetora se cada elemento do domínio é mapeado para um elemento único na imagem.
Em outras palavras, diferentes elementos do domínio resultam em diferentes elementos na imagem. Um diagrama representaria uma seta saindo de cada elemento de A e apontando para um único elemento em B, sem que duas setas apontem para o mesmo elemento de B. Exemplo: f(x) = 2x, onde cada x possui uma imagem única.Uma função é sobrejetora se todo elemento do contradomínio (imagem) é imagem de pelo menos um elemento do domínio.
Em um diagrama, isso significaria que todas as ‘bolinhas’ em B receberiam pelo menos uma seta vinda de A. Exemplo: f(x) = x² (considerando apenas os reais positivos como contradomínio).Uma função é bijetora se for simultaneamente injetora e sobrejetora. Em um diagrama, isso significaria que cada elemento de A está conectado a exatamente um elemento de B, e vice-versa.
Exemplo: f(x) = x (função identidade). Uma função bijetora garante a existência de uma função inversa.
Domínio, Contradomínio e Imagem
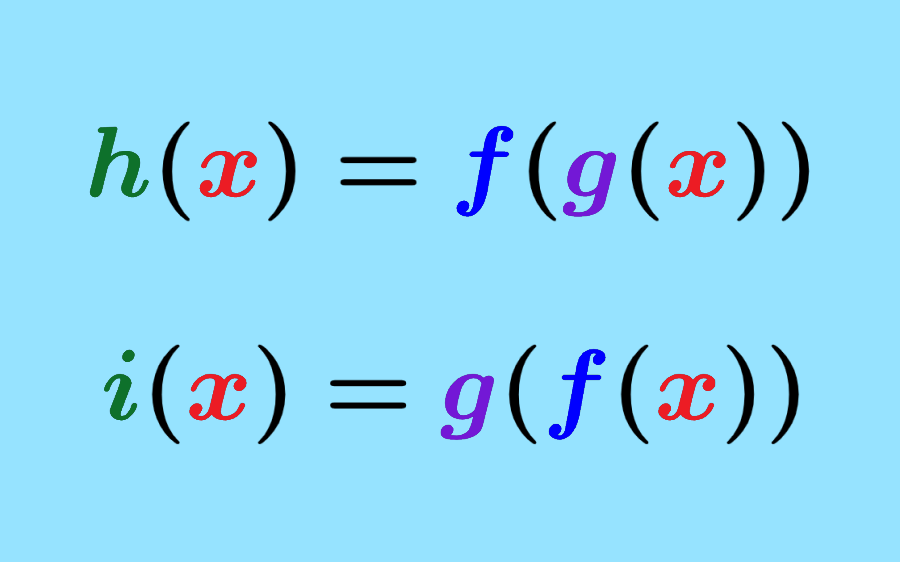
Compreender domínio, contradomínio e imagem é fundamental para o trabalho com funções matemáticas. Esses conceitos definem o conjunto de valores possíveis de entrada, saída e os valores efetivamente assumidos pela função, respectivamente. Dominar esses conceitos permite uma análise completa do comportamento de uma função.
Definições de Domínio, Contradomínio e Imagem
O domínio de uma função é o conjunto de todos os valores possíveis que a variável independente (geralmente representada por x) pode assumir. Em outras palavras, é o conjunto de valores para os quais a função está definida. O contradomínio, por sua vez, é o conjunto de todos os valores possíveis que a variável dependente (geralmente representada por y ou f(x)) pode assumir.
Finalmente, a imagem de uma função é o subconjunto do contradomínio que contém todos os valores efetivamente assumidos pela função, ou seja, os valores de y que são obtidos para algum x no domínio.Consideremos a função f(x) = x². O domínio desta função é o conjunto de todos os números reais, pois podemos calcular o quadrado de qualquer número real.
O contradomínio também é o conjunto dos números reais, uma vez que o quadrado de um número real pode resultar em qualquer número real não-negativo. A imagem, porém, é o conjunto dos números reais não-negativos (R+), pois o quadrado de qualquer número real é sempre não-negativo.Como exemplo com restrição no domínio, consideremos a função g(x) = 1/x. Aqui, o domínio é o conjunto de todos os números reais exceto zero (R – 0), pois a divisão por zero é indefinida.
O contradomínio é o conjunto de todos os números reais, e a imagem também é o conjunto de todos os números reais, exceto zero.
Exercício: Determinação do Domínio, Contradomínio e Imagem

Determine o domínio, contradomínio e a imagem da função h(x) = √(x – 1). Resolução:
1. Domínio
A raiz quadrada só está definida para valores não negativos. Portanto, x – 1 ≥ 0, o que implica x ≥ 1. Assim, o domínio é o intervalo [1, ∞).
2. Contradomínio
Como a função envolve uma raiz quadrada, os valores de h(x) serão sempre não-negativos. Portanto, o contradomínio é o conjunto dos números reais não-negativos, [0, ∞).
3. Imagem
A função h(x) = √(x – 1) assume todos os valores não-negativos quando x ≥ 1. Portanto, a imagem é o intervalo [0, ∞).
Exemplos Resolvidos, Exercícios Sobre Definição De Função – Exercícios Mundo Educação
| Função | Domínio | Imagem |
|---|---|---|
| f(x) = x² | (-∞, ∞) | [0, ∞) |
| g(x) = 1/x | (-∞, 0) U (0, ∞) | (-∞, 0) U (0, ∞) |
| h(x) = √(x – 1) | [1, ∞) | [0, ∞) |
Representação de Funções e Operações
Este tópico aborda a representação gráfica de funções, focando em funções lineares e quadráticas, e detalha as operações aritméticas com funções, incluindo a composição e inversão de funções. A compreensão dessas representações e operações é fundamental para o domínio da análise de funções.
Representação Gráfica de Funções

A representação gráfica de uma função permite visualizar seu comportamento e identificar propriedades importantes, como crescimento, decrescimento e pontos de intersecção com os eixos coordenados. Para funções lineares, representadas por f(x) = ax + b, o gráfico é uma reta. Para funções quadráticas, representadas por f(x) = ax² + bx + c, o gráfico é uma parábola.Para construir o gráfico de uma função, precisamos determinar alguns pontos que satisfazem a equação da função.
Por exemplo, para a função linear f(x) = 2x + 1, podemos escolher alguns valores para x (por exemplo, -1, 0, 1, 2) e calcular os correspondentes valores de f(x): f(-1) = -1, f(0) = 1, f(1) = 3, f(2) = 5. Plotando esses pontos (x, f(x)) em um plano cartesiano e traçando uma reta que passa por eles, obtemos o gráfico da função.
Para uma função quadrática como f(x) = x²2x + 1, o processo é semelhante, porém o gráfico resultante será uma parábola. Devemos encontrar o vértice da parábola (ponto de mínimo ou máximo) e alguns outros pontos para traçar a curva. O vértice pode ser encontrado usando a fórmula x = -b/2a.
Operações com Funções
As operações aritméticas (soma, subtração, multiplicação e divisão) podem ser aplicadas a funções, resultando em novas funções. Considere duas funções, f(x) e g(x).
Soma de Funções
A soma de duas funções, (f + g)(x), é definida como (f + g)(x) = f(x) + g(x). O domínio da função resultante é a intersecção dos domínios de f(x) e g(x).
A soma de funções preserva a linearidade: se f(x) e g(x) são lineares, (f+g)(x) também será linear.
Subtração de Funções
A subtração de duas funções, (f – g)(x), é definida como (f – g)(x) = f(x)g(x). O domínio da função resultante é a intersecção dos domínios de f(x) e g(x).
Multiplicação de Funções
A multiplicação de duas funções, (f
- g)(x), é definida como (f
- g)(x) = f(x)
- g(x). O domínio da função resultante é a intersecção dos domínios de f(x) e g(x).
Divisão de Funções
A divisão de duas funções, (f / g)(x), é definida como (f / g)(x) = f(x) / g(x), desde que g(x) ≠ 0. O domínio da função resultante é a intersecção dos domínios de f(x) e g(x), excluindo os valores de x para os quais g(x) = 0.
Na divisão de funções, é crucial garantir que o denominador não seja zero, para evitar a indeterminação.
Funções Compostas e Funções Inversas
Funções compostas e funções inversas representam diferentes operações com funções.
Funções Compostas
Uma função composta é criada aplicando uma função à saída de outra função. Se temos duas funções f(x) e g(x), a função composta (f o g)(x) é definida como (f o g)(x) = f(g(x)). O domínio da função composta é o conjunto de valores de x para os quais g(x) está no domínio de f(x).Exemplo: Se f(x) = x² e g(x) = x + 1, então (f o g)(x) = f(g(x)) = (x + 1)².
Funções Inversas
Uma função inversa, denotada por f⁻¹(x), “desfaz” o efeito de uma função f(x). Se f(a) = b, então f⁻¹(b) = a. Nem todas as funções possuem uma inversa. Para que uma função tenha inversa, ela deve ser bijetora (injetora e sobrejetora). O domínio da função inversa é o contradomínio da função original, e vice-versa.Exemplo: Se f(x) = 2x + 1, então sua inversa é f⁻¹(x) = (x – 1)/2.
Observe que f(f⁻¹(x)) = x e f⁻¹(f(x)) = x.
Concluindo nossa jornada pelos Exercícios Sobre Definição De Função – Exercícios Mundo Educação, percebemos a importância de uma compreensão sólida dos diferentes tipos de funções e suas propriedades. De linear a exponencial, de injetora a bijetora, cada conceito se conecta formando um todo coeso e fundamental para a matemática. Ao dominarmos o domínio, contradomínio e imagem, e as operações entre funções, abrimos portas para um mundo de aplicações práticas e um entendimento mais profundo dos princípios matemáticos.
Pratique, explore e continue aprendendo!

