Circuitos Hamiltonianos: Uma Exploração: Como Se Dá O Funcionamento Do Circuito Hamiltoniano Cite Exemplos

Como Se Dá O Funcionamento Do Circuito Hamiltoniano Cite Exemplos – Este artigo explora o conceito de circuitos hamiltonianos, algoritmos para sua descoberta, aplicações em diferentes contextos, exemplos de grafos sem circuitos hamiltonianos e a complexidade computacional associada à sua busca. A compreensão dos circuitos hamiltonianos é crucial em diversas áreas, desde a otimização de rotas até a biologia computacional.
Introdução ao Circuito Hamiltoniano
Um circuito hamiltoniano em um grafo é um ciclo que visita cada vértice exatamente uma vez, retornando ao vértice de origem. Diferencia-se de um caminho hamiltoniano, que também visita todos os vértices exatamente uma vez, mas não retorna ao ponto de partida. Para entender melhor, precisamos definir alguns termos essenciais: vértices representam os pontos ou nós do grafo; arestas são as conexões entre os vértices; e o grau de um vértice é o número de arestas conectadas a ele.
Algoritmos para Encontrar Circuitos Hamiltonianos
Existem diversos algoritmos para encontrar circuitos hamiltonianos, porém a maioria deles possui complexidade computacional muito alta. Dois algoritmos comuns são o algoritmo de força bruta e algoritmos heurísticos. O algoritmo de força bruta testa todas as possíveis permutações de vértices, sendo extremamente ineficiente para grafos grandes. Algoritmos heurísticos, por outro lado, buscam soluções aproximadas, mais rápidas, mas sem garantia de encontrar a solução ótima.
A seguir, apresentamos os passos de um algoritmo de busca exaustiva (força bruta), adaptado para melhor visualização em tabela:
| Passo | Descrição | Exemplo (grafo com 4 vértices) | Observação |
|---|---|---|---|
| 1 | Gere todas as permutações possíveis dos vértices. | (A, B, C, D), (A, B, D, C), (A, C, B, D), … | O número de permutações cresce exponencialmente com o número de vértices. |
| 2 | Para cada permutação, verifique se forma um circuito. | Verifique se existe uma aresta entre cada par de vértices consecutivos na permutação, e se existe uma aresta entre o último e o primeiro vértice. | Isto envolve checar a existência de todas as arestas necessárias no grafo. |
| 3 | Se a permutação formar um circuito, retorne-o. | Se todas as arestas existirem, a permutação representa um circuito hamiltoniano. | Caso contrário, continue para a próxima permutação. |
| 4 | Se nenhuma permutação formar um circuito, retorne “Não existe circuito hamiltoniano”. | Se todas as permutações forem testadas sem encontrar um circuito, o grafo não possui um circuito hamiltoniano. | Este é o caso para muitos grafos. |
Exemplo de aplicação em um grafo com 4 vértices (A, B, C, D) onde as arestas são: AB, BC, CD, DA. O algoritmo testaria permutações como (A,B,C,D). Como existe a aresta AB, BC, CD e DA, esta permutação representa um circuito hamiltoniano.
Exemplos de Circuitos Hamiltonianos em Diferentes Contextos
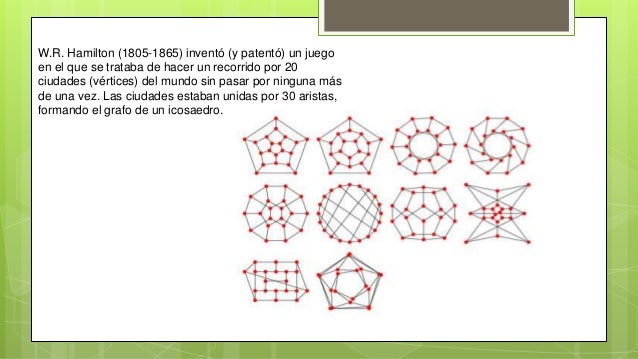
Circuitos hamiltonianos encontram aplicações em diversos campos. A seguir, apresentamos três exemplos:
- Logística: O problema de encontrar a rota mais eficiente para um caminhão de entregas visitar vários locais.
- Os vértices representam os locais de entrega.
- As arestas representam as rotas entre os locais.
- Um circuito hamiltoniano representa a rota que visita todos os locais exatamente uma vez e retorna ao ponto de partida.
- Roteamento de Veículos: Otimização de rotas para veículos de transporte público, como ônibus ou trens, que precisam visitar várias paradas.
- Os vértices representam as paradas.
- As arestas representam as rotas entre as paradas.
- Um circuito hamiltoniano garante que todos os pontos sejam visitados eficientemente.
- Biologia Computacional: Sequenciamento de genomas, onde é necessário determinar a ordem dos genes em um cromossomo.
- Os vértices representam os genes.
- As arestas representam as relações entre os genes.
- Um circuito hamiltoniano pode auxiliar na reconstrução da ordem correta dos genes.
Em todos os exemplos, os grafos podem variar em tamanho, densidade e estrutura, dependendo da aplicação específica. Porém, a busca por um circuito hamiltoniano representa a otimização de um percurso que visita todos os pontos relevantes exatamente uma vez.
Grafos que Não Possuem Circuitos Hamiltonianos, Como Se Dá O Funcionamento Do Circuito Hamiltoniano Cite Exemplos
Nem todos os grafos possuem circuitos hamiltonianos. Um grafo com um vértice de grau 1, por exemplo, não pode possuir um circuito hamiltoniano, pois um circuito precisa retornar ao ponto de partida. Grafos com muitos vértices de grau baixo também dificultam a existência de um circuito hamiltoniano.
Exemplo: Um grafo com cinco vértices (A, B, C, D, E) com as seguintes arestas: AB, AC, AD, AE, BC, BD, BE. Este grafo não possui um circuito hamiltoniano porque o vértice A está conectado a todos os outros vértices, criando um “estrela” e impossibilitando um ciclo que inclua todos os vértices sem repetição.
Representação visual de um grafo sem circuito hamiltoniano: Imagine um grafo com 5 vértices dispostos em uma estrela, com um vértice central (A) conectado a quatro vértices externos (B, C, D, E). Os vértices externos não são conectados entre si. Este grafo não possui circuito hamiltoniano porque qualquer tentativa de criar um ciclo que passe por todos os vértices irá necessariamente repetir o vértice central (A).
Complexidade Computacional da Busca de Circuitos Hamiltonianos
Encontrar um circuito hamiltoniano é um problema NP-completo. Isso significa que o tempo necessário para encontrar uma solução cresce exponencialmente com o tamanho do grafo. Para grafos pequenos, a busca exaustiva pode ser viável, mas para grafos grandes, torna-se computacionalmente inviável. Devido a essa alta complexidade, algoritmos heurísticos e aproximados são frequentemente utilizados na prática, buscando soluções razoáveis em tempo aceitável, mesmo que não sejam ótimas.
O que acontece se um grafo não possuir um circuito hamiltoniano?
Se um grafo não possuir um circuito hamiltoniano, significa que não existe um caminho que visite todos os seus vértices exatamente uma vez e retorne ao ponto de partida. Neste caso, outras estratégias de otimização devem ser consideradas.
Quais são as aplicações do conceito de circuito hamiltoniano na inteligência artificial?
O conceito é usado em algoritmos de busca, planejamento de rotas em robótica e na resolução de problemas de satisfação de restrições (CSP).
Existe um algoritmo que garante encontrar um circuito hamiltoniano em tempo polinomial?
Não. Encontrar um circuito hamiltoniano é um problema NP-completo, o que significa que não se conhece um algoritmo eficiente (tempo polinomial) para resolvê-lo em todos os casos.

